こんにちは！

リバネスの西山です。

今日は、奈良県立青翔中学校・高等学校に行ってきました！

遺跡のモモ核から日本のモモのルーツにせまる ( 奈良県立青翔高等学校 探究生物班 )

我々は、奈良県の纏向遺跡（3世紀半ごろ）と名柄遺跡（５世紀後葉）から出土したモモ核を形態により分類した。この纏向遺跡のモモ核は卑弥呼の時代のものであり、名柄遺跡は葛城氏最後の盟主円大臣の館跡と言われている。長さ・幅・厚さを測定し、長さ／幅、長さ／厚さ、幅／厚さの比から分類した。その結果、纏向遺跡のモモ核は１種類、名柄遺跡のモモ核は2種類であることがわかった。纏向遺跡のモモ核と名柄遺跡のモモ核は1種類が同じであったため、およそ200年以上も同じモモが利用されていたと考えられる。名柄遺跡の他方のモモ核は5世紀中ごろから、須恵器と共に急に出土することから、朝鮮半島から持ち込まれたと考えられる。

田んぼは発電する ( 奈良県立青翔高等学校 探究科学生物発電班 )

奈良県内3地点の水田の泥を15Lのバケツにいれ、イネ（ヒノヒカリ）を栽培した。そのバケツに炭素棒を電極にして、片方は泥の中、もう一方は水中においた。その結果、電圧は高いバケツで0.6Vまで上昇し、イネと光があることが起電力を高くし、田んぼは発電することがわかった。一般的な微生物燃料電池1つは0.3Vほどなので、本研究の電圧は高いといえる。泥の中に発電菌が存在することは知られており、発電菌が発電したと考えた。また、イネと光がある方が起電力は高いため、光合成産物を発電菌が利用している可能性がある。今後は外部電源のない山奥などの水田でイノシシよけのLEDを点滅させることを考えている。

コラッツ問題に類するaｎ+bを考察する ( 奈良県立青翔高等学校 sshコース2年4組数学M2班 )

コラッツ問題とは、「正の数nをとり、これが奇数なら3倍して1を加える。偶数なら2で割る。これを繰り返すとはじめにどんなnを選んでも、いつかは1→4→2→1を繰り返す」。このことは、nが4兆まではコンピューターで確かめられてるが、数学的に証明されておらず未解決問題である。我々はこの問題の偶数と奇数の場合分けを拡張した操作を考え（例、nが3で割り切れるなら3で割る。nが3で割ると1余るなら4倍して1を引き、2余るなら4倍して2を引く）数値実験を行いコラッツ問題にせまる。

変化アサガオの秘密にせまる ( 奈良県立青翔中学校 1年有志 )

アサガオの野生型は青く丸い花と三つに尖る葉である。しかし、我々が栽培した変化アサガオ4品種には、柳の葉の様に細長い葉を持つ株、リンドウやナデシコの様な形態の花をつける株などが出現した。同じ品種の種子から3種類の花と2種類の葉をもつ株が2品種、3種類の花と1種類の葉が1品種に出現した。種子を形成しない株があり、葉は柳葉、花弁が深裂し、子房がなく、柱頭が３裂するとわかった。花弁の深裂する個体は柱頭も3裂することから、花弁の深裂と柱頭の3裂は同じ遺伝子が関係すると考えた。また、花弁が表側へ巻き込む株は、葉の表裏の気孔の数がほぼ同数であることから、葉と花弁の形成時に表裏の軸に変異があると考えられる。

もうここまでで、この学校の凄まじさが伝わってきますね。
モモ核と田んぼ発電の2件が口頭発表審査をくぐり抜け、さらにコラッツ問題と変化アサガオがポスター発表。
1校で4テーマもの発表です。

（ちなみに学校には他にも天文や植生に関するポスターも掲示されており、まだまだネタがある様子でした・・・恐るべし）

というわけで、4件もの発表を聞くため、サクサクと進めていきます。

第一弾は、モモ核。

日本の歴史を科学的な視点で紐解く、おもしろい研究でした。
が、、、惜しかったのは、その背景の説明不足。
最後まで聞いてみると、「なるほど！」と思えたものの、 最初にその魅力が伝わってこない。
そうすると、そもそも話を聞いてもらえない可能性があるわけですね。

そういうわけで、このチームに行ったアドバイスは、

「聞いている人はみんなシロウトだから、特に入り口の部分はわかりやすいストーリーを話すべし」

ということと、

「一目見て“ここが違うんだ”と聴衆が理解できるように結果を提示しよう」

ということ。

第二弾は田んぼ発電。

なんのこっちゃら？とに思えるかもしれませんが、地元の農家さんが抱える課題を解決する
ナイスアイデアな研究でした。

こちらのチームに伝えたのは、
「結果に対して誠実であるべし」

実は結果のまとめとして表現されたことと、一部異なるデータが出ていたんですね。
そうしたデータがなぜ得られたのか、原因を検証するためにどのような実験を行えばいいのかを
考えてもらいたいです。

また、実験のコントロール設計にももうひと工夫できそうだったので、その点についてもアドバイス。

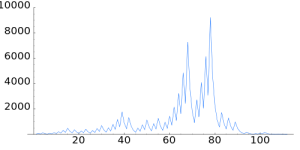
さて第三弾のコラッツ問題。

by Pokipsy76

コラッツ予想という、いまだ数学界において 証明がなされていない問題があり、
それを解き明かすための一歩目として数式の一般化およびパターンの探索を行ったものです。

私も数学は専門外なわけですが、グラフの意味が理解できるとそこまで難解な話ではない、、、という感じでした。

が、説明の中でグラフの見方をわかりやすく伝えていなかったので、そこをアドバイス。

「ポスターには、説明しなくても分かるだけの情報量を込める」のがポイントですね。

そして最後。変化アサガオ。

こちらは様々な変化アサガオの写真が必見です！
ただ、種類が多く、花弁だけでなく葉や雌しべ、雄しべなど様々な部位を観察し、写真を撮っていたので、
その結果の提示の仕方で苦労していました。

ここで行ったアドバイスは、「うまく表形式にして、見やすく並べる」テクニックです。

品種名を縦の列、花弁や葉等の形質を横の行にして並べると、異なる品種の形質同士、
または品種の中での形質を見比べやすくなるのです。

最後に。
おどろくべきことに、学校内でイノシシが飼育されていました。
実験用とのことで、様々な色の光に対する反応性などを見ているそうです。

以上です！　（西山）

ポイントまとめ

⑦結果の見せ方を工夫して、どこをどう見ればいいのかを迷わない作りにしよう。

⑧得られた結果は、基本的に正しい。それを説明付けるための仮説をどう立てられるか、現時点で立てられないなら、どんな追加実験を行えばいいかを考えよう。