便利な現代、私たちは家にいながらにしてインターネットで買い物を楽しむことができます。この際、クレジットカードの番号や住所、氏名、電話番号といった、悪意をもった人には知られたくない重要な情報をやり取りする必要があります。この情報はどのように守られているのでしょうか？そこで登場するのが、情報を、特別な知識（鍵）がないと内容がわからないように暗号文に変換する「暗号化」です。個人情報の流出など、情報セキュリティの重要性が問われる昨今、私たちの生活に密接したセキュリティを支える暗号と、それを支える数学の動向を最新の論文から読み解いてみましょう。

暗号の安全を左右する、鍵の受け渡し

暗号の歴史は紀元前3000年バビロニア時代の象形文字に始まったと言われています。当時、文字は特別な教育を受けた一部の人間にしか読めなかったため、大多数の人にとっては暗号だったといえます。 そこで「文字」という鍵を使って、情報の暗号化（文字化）と解読が行われました。時代が進むと、「道具」を使った暗号化が行われるようにな ります。古代ギリシアのスキュタレー暗号は、決められた太さの棒と、 細長い紙を使って作られる暗号で、棒に巻きつけて書いた紙を棒から外すことで暗号化し、紙を同じ太さの棒に巻きつけることで解読します。19世紀に入ると、手作業だった暗号化、解読に「機械」が使われるようになり、暗号の解読は飛躍的に困難になりました。機械式暗号化 装置として有名なのが、第二次世界大戦時、ナチス・ドイツ軍が用い た「エニグマ」です。エニグマは歯車を利用して、入力文字を対応する文字に置き換える換字式の暗号化装置です。スキュタレー暗号やエニグマのように、棒や装置など、同じ仕組み（鍵）で暗号化と解読を行う方式は「共通鍵暗号」と呼ばれ、1970年代まで暗号化の主要な方法で した。しかし、共通鍵暗号は暗号の送信者と受信者が鍵のやり取りを行う必要があり、鍵が途中で盗まれる心配がありました。鍵の受け渡しには常に細心の注意を払わなくてはならず、情報通信の増加とともに、その手間が大きな問題となっていきました。

辿り着いた「RSA暗号」と、迫る量子計算の脅威

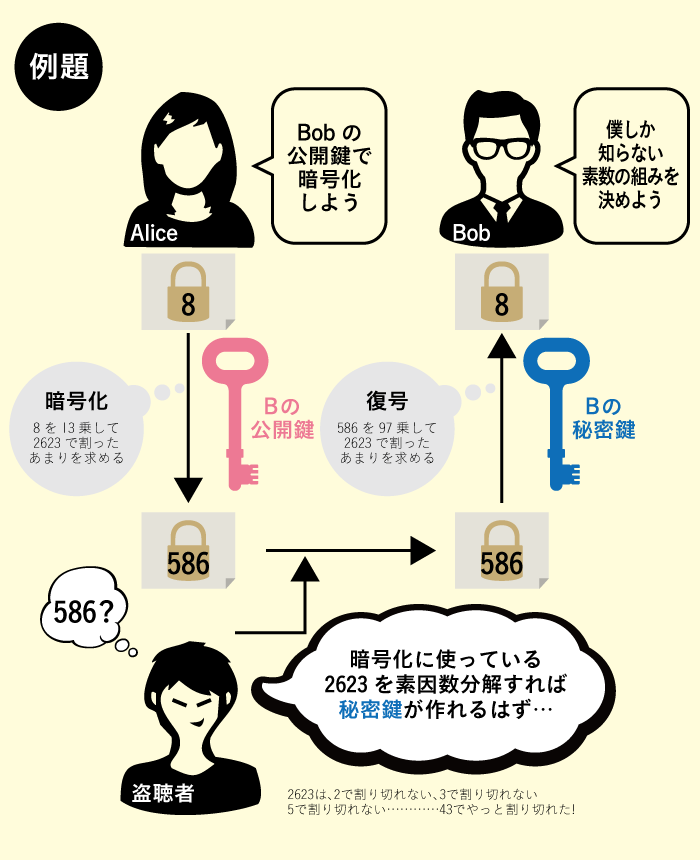
この問題を解決に導いたのが、数学を応用した暗号である「公開鍵暗号」方式です。この方式の特徴は、暗号化と解読を、別々の鍵で行うことです。暗号化するのに使う鍵を「公開鍵」といい、例えばAliceがBobに秘密のメッセージを送りたい時には、Bobが公開している公開鍵を使って、メッセージを暗号化します。誰でも知ることができる公開鍵 は、メッセージを暗号化することはできますが、解読することはできません（正確には、解読にとても時間がかかります。後述参照）。誰にでも閉められる南京錠のようなものです。暗号を解読するには、Bobだけが持っている「秘密鍵」を使う必要があります。これは南京錠の鍵のようなものです。公開鍵暗号方式にすることで、秘密鍵をやり取りする必要がなくなり、秘密鍵が盗まれて暗号が解読される心配が格段に少なくなりました。公開鍵暗号の方式でもっともよく使われているのがRSA暗号（開発者Rivest氏、Shamir氏、Adleman氏の頭文字）で、この方式には「素因数分解の困難性」が使われています。これは「素数同士の掛け算は簡単だが、掛け算の結果から、元の素数を導き出すのは非常に難しい」という数学的な特徴です（AliceとBobの例題を参照）。RSA暗号を秘密鍵なしで解読しようとすると、約600桁の整数を素因数分解しなければなりません。世界一の性能を誇るスーパーコンピュータを用いてもこれを素因数分解するのに10,000年以上かかると言われています。解読し終わった頃には情報の価値がなくなってしまっているため、現実的に暗号化された情報は安全であると言われています。つまり、「計算に時間がかかる」ということが暗号の安全性を支えているのです。
しかし、これはコンピュータの計算が速くなればRSA暗号は解読されることを意味します。近年、スーパーコンピュータの何億倍もの計算速度を誇る量子コンピュータの実用化の波が迫っています。量子コンピュータによって、暗号の全てが解読されてしまうかもしれないという危惧が急速に募っており、対応できる新たな暗号が求められていました。

計算力を凌駕する、数学の「鍵」

圧倒的な計算速度を誇る量子コンピュータの登場で、全ての暗 号は解読されてしまうのでしょうか。実は近年、量子コンピュー タでも解読困難な暗号が、数学を応用して開発されています。
そのひとつが、「格子暗号」です。格子暗号とは、空間内に規則的に並んだ点の集まり（格子）の数学的な性質を使った暗号です。その性質の一つには「Learning with Errors問題」と呼ばれる数学の問題が使われています。これは、解けるように作られた大量の方程式に、誤差（Errors）の項を追加して作った近似方程式

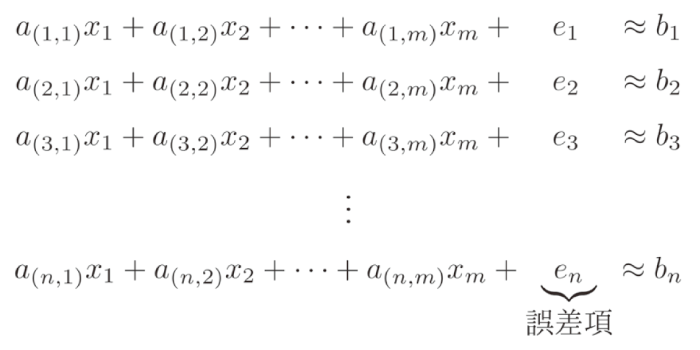
を解く問題で、誤差の情報なしにこの近似された方程式を解く（x₁, x₂・・・x_mを求める）ことは非常に困難であるという性質をもっています。格子暗号は、RSA暗号に比べて秘密鍵の情報量が数倍から数兆倍に大きくなるという欠点はありますが、量子コンピュータをもってしても未だに現実的な時間で解く方法が見つかっていません。この暗号は、安全性が高い暗号として現在、世界中で実証実験が行われています。

メイド・イン・ジャパンの新暗号

実際に暗号を社会実装するときには様々な問題に直面します。例え ば、データ送信中に起こるデータの破損や悪意ある人による傍受です。 この問題に対処するには、送信時と受信時のデータに変化がなかったかどうかをチェックする必要があります。
実は、このチェック機能を搭載した新しい暗号は日本でも研究されており、2018年、ついに国立研究開発法人情報通信研究機構（NICT）によって開発されました。LOTUSと名付けられたこの暗号もLearning with Errors問題を採用した格子暗号で、耐量子性をもっているだけでなく、安全性チェック機構も備わっています。データを暗号化する際、暗号文と一緒にその構造情報もパッキングします。そして、解読時に暗号文と構造情報が一致しているかをチェックする仕組みになっており、もし、不一致の箇所が見つかれば、復号を中断するようになっています。世界標準の暗号技術の候補にノミネートされていることもあり、現実的な時間で解読可能な解き方や悪意あるユーザから傍受される仕組みが存在しないか、既存のシステムへの実装が容易かなどの観点で、世界中で研究が行われています。
インターネットなどの通信手段や科学技術が発展することで、生活が便利になると同時に、個人情報が他人に漏洩する危険性も増えてきました。私たちの大切な情報を守ってくれる数学と暗号の発展から、今後も目が離せません。